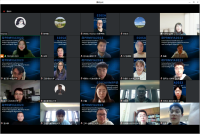
Today, I presented the keynote speech Frequency Fitness Assignment [频率适应度分配] on 2023-03-25 at the 2023 International Conference on Pattern Recognition, Machine Vision and Intelligent Algorithms (PRMVIA) conference. The conference took place online and was very well attended, very well organized, and had an exciting program that offered several interesting talks and workshops. The keynote focuses on Frequency Fitness Assignment (FFA), an algorithm module that can be plugged into existing optimization algorithms. FFA prevents premature convergence to local optima and makes algorithms invariant under all injective transformations of the objective function value. This interesting feature is explained in comparison to the invariance properties of the (1+1) EA, Simulated Annealing, and Genetic Algorithms. Several results of FFA are presented. The talk is also available on our website, both as slides pdf and as forty-minute video.
Abstract
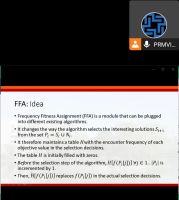
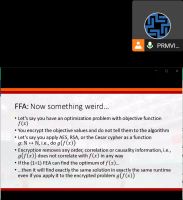
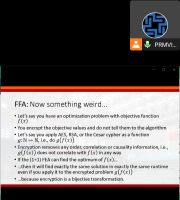
Optimization problems are situations where we have to pick one of many possible choices and want to do this in such a way that we reach a pre-defined goal at a minimum cost. Classical optimization problems include the Traveling Salesperson Problem, the Maximum Satisfiability Problem (MaxSat), and the Bin Packing problem, for example. Since these problems are NP-hard and solving them to optimality would require exponential runtime in the worst case, metaheuristic algorithms have been developed that deliver near-optimal solutions in acceptable runtime. Examples for classical metaheuristics are the (1+1) EA (also known as randomized local search), Simulated Annealing (SA), and the Standard Genetic Algorithm (SGA). Since we want that such algorithms should behave the same both in quick benchmarking experiments and in practical applications, we would like them to exhibit invariance properties. SA, however, is not invariant under scaling of the objective function and the SGA with fitness-proportionate selection is not invariant under translations of the objective function. The (1+1) EA is invariant under all order-preserving transformations of the objective function value. All heuristic optimization methods are biased to prefer, or at least to select with higher average probability, better solutions over worse ones in their sampling process. They therefore cannot have any stronger invariance property that the (1+1) EA. Frequency Fitness Assignment (FFA) is an algorithm module that can be plugged into existing algorithms. It makes them invariant under all injective transformations of the objective function value, which goes far beyond order-preserving transformations (encryption is, for instance, a bijective transformation…). FFA allows for efficient optimization without bias towards better solutions. We plug FFA into the (1+1) EA. We show that the resulting (1+1) FEA can solve the non-NP-hard Trap, TwoMax, and Jump problems in polynomial runtime, whereas the (1+1) EA needs exponential runtime. Moreover, the (1+1) FEA performs significantly faster on the NP-hard MaxSat problem. We conclude the presentation with an outline of other properties of FFA and our other recent works.
Photos
Keynote Talk
This is the forty-minute talk given on March 25, 2023, at the PRMVIA conference. Here you can download the slides PDF (in English). A similar talk was given on 2023-04-06 at the Harbin Institute of Technology in Shenzhen, Guangdong, China [哈尔滨工业大学(深圳)].